Chapter 27 Working with frequencies
27.1 Introduction
Much of the time in biology we are dealing with whole objects (plants, animals, cells, eggs, islands, etc.) or discrete events (attacks, matings, nesting attempts, etc.). We are often interested in making measurements of numeric variables (length, weight, number, etc.) and then either comparing means from samples (e.g. mean leaf size of plants from two habitat types), or investigating the association between different measurements (e.g. mean leaf size and herbivore damage).
However, we sometimes find a situation in which the ‘measurement’ we are interested in is not a quantitative measure, but is categorical. Categorical data are things like sex, colour or species. Such variables cannot be treated in the same way as numeric variables. Although we can ‘measure’ each object (e.g. record if an animal is male or female), we can’t calculate numeric quantities such as the ‘mean colour morph’, ‘mean species’ or ‘median sex’ of animals in a sample. Instead, we work with the observed frequencies, in the form of counts, of different categories, or combinations of categories.
27.2 A new kind of distribution
There are quite a few options for dealing with categorical data23. We’re just going to look at one option in this book: \(\chi^2\) tests. This is pronounced, and sometimes written, ‘chi-square’. The ‘ch’ is a hard ‘ch’, as in ‘character’. This isn’t necessarily the best approach for every problem, but \(\chi^2\) tests are widely used in biology so they are a good place to start.
It is not critical that you understand everything in this section. This material is here to help those who like to have a sense of how statistical tests work. You won’t be assessed on it.
The \(\chi^2\) tests that we’re going to study borrow their name from a particular theoretical distribution, called… the \(\chi^2\) distribution. We don’t need to study this in much detail. However, just as with the normal distribution and the t-distribution, it can be helpful to know a little bit about it.
The \(\chi^2\) distribution pops up a lot in statistics. However, in contrast to the normal distribution, it isn’t often used to model the distribution of a variable we’ve sampled (i.e. ‘the data’). Instead, the \(\chi^2\) distribution is often associated with a test statistic of some kind.
The standard \(\chi^2\) distribution is completely described by only one parameter, called the degrees of freedom. This is closely related to the degrees of freedom idea introduced in the chapters on t-tests.
The \(\chi^2\) distribution is appropriate for positive-valued numeric variables. Negative values can’t be accommodated. This is because the distribution arises whenever we take one or more normally distributed variables, square these, and then add them up.
Let’s take a look at the \(\chi^2\) distribution with one degree of freedom:
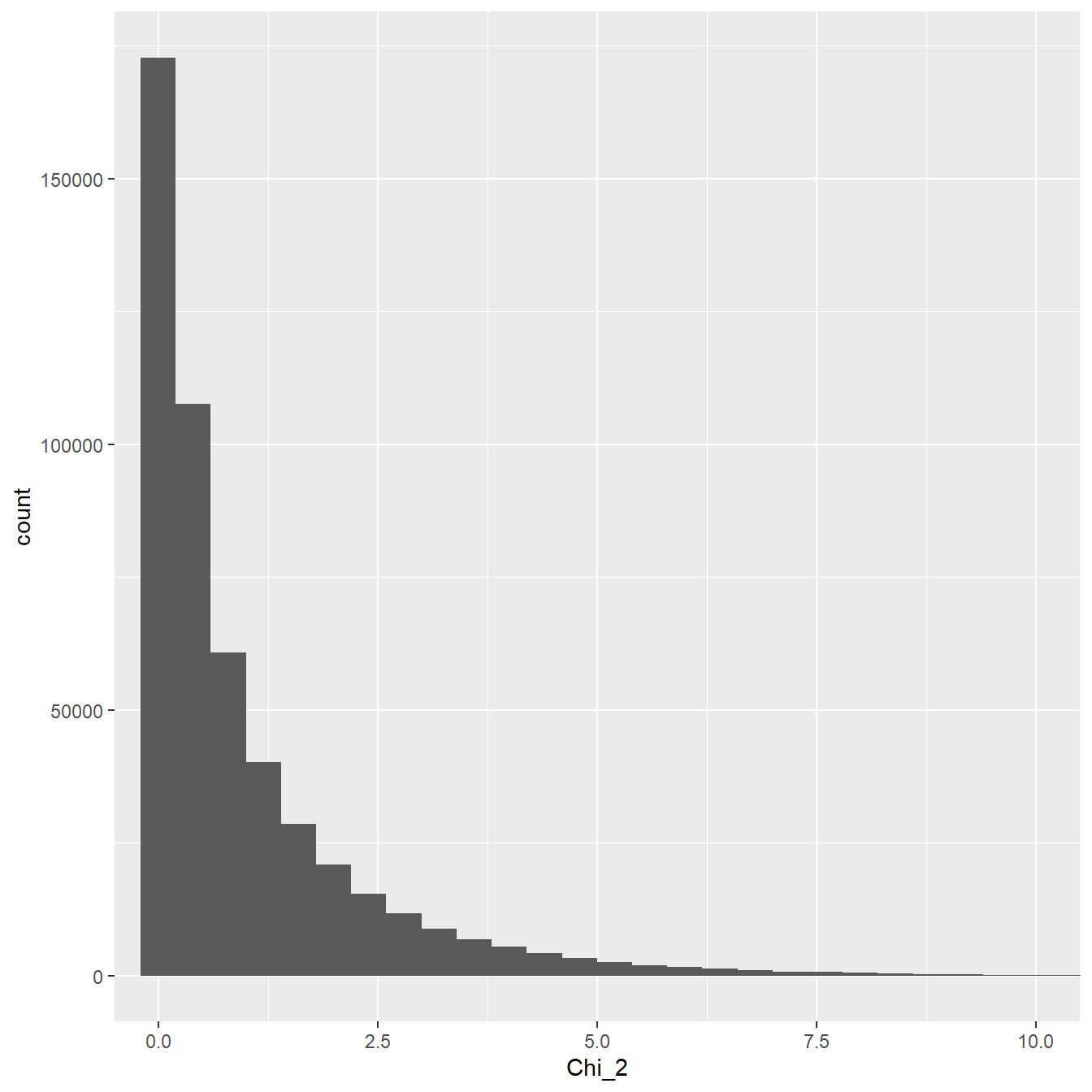
Figure 27.1: Distribution of a large sample of chi-square distributed variable with one degree of freedom
As we just noted, only positive values occur and most of these values lie between about 0 and 10. We can also see that the distribution is asymmetric. It is skewed to the right.
So why is any of this useful?
Let’s look at the plant morph example again. Imagine that we are able to take repeated samples from a population when the purple morph frequency is 25% . Let’s take repeated samples of 1000 plants each time. If the true frequency is 25% we expect to sample 250 purple plants each time. We’ll call this number the ‘expected value’. We won’t actually end up with 250 plants in each sample because of sampling error. We’ll call this latter number the ‘observed value’.
So far we’re not doing anything we haven’t seen before. We’re just trying to see what happens under repeated sampling from a population. Here’s the new bit… Imagine that every time we sample the 1000 plants, we calculate the following test statistic…
\[2*\frac{(O-E)^{2}}{E}\]
…where \(O\) is the observed value and \(E\) is the expected value defined above. What does the distribution of this test statistic look like? We can find out by simulating the scenario in R and plotting the results:
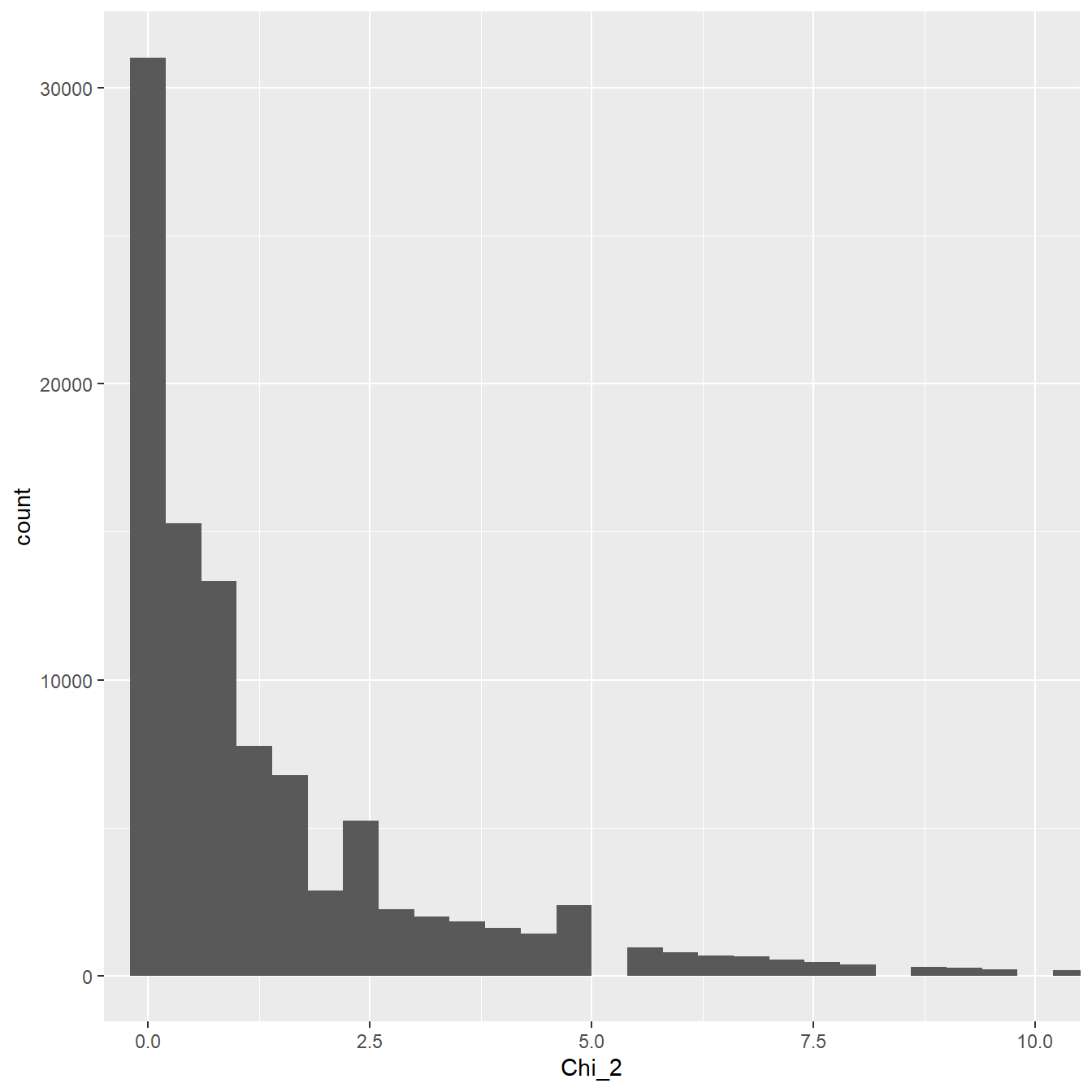
Figure 27.2: Distribution of the test statistic
That looks a lot like the theoretical \(\chi^2\) distribution we plotted above. It turns out that observed frequencies (‘counts’) that have been standardised with respect to their expected values—via the \(\frac{(O-E)^{2}}{E}\) statistic—have a \(\chi^2\) sampling distribution (at least approximately). This result is the basis for using the \(\chi^2\) distribution in various statistical tests involving categorical variables and frequencies.
27.3 Types of test
We’re going to learn about two different types of \(\chi^2\) test. Although the two tests work on the same general principle, it is still important to distinguish between them according to where they are used.
27.3.1 \(\chi^{2}\) goodness of fit test
A goodness-of-fit test is applicable in a situation where we have a single categorical variable and some hypothesis from which we can predict the expected proportions of observations falling in each category.
For example, we might want to know if there is any evidence for sex-related bias in the decision to study biology at Sheffield. We could tackle this questions by recording the numbers of males and females in a cohort. This would produce a sample containing one nominal variable (Sex) with only two categories (Male and Female). Based on information about human populations, we know that the sex ratio among 18 year olds is fairly close to 1:124. We are thus able to compare the goodness of fit of the number of males and females in a sample of students with the expected value predicted by the 1:1 ratio.
If we had a total of 164 students we might get this sort of table:
| Male | Female | |
|---|---|---|
| Observed | 64 | 100 |
With a 1:1 sex ratio, if there is no sex-bias in the decision to study biology, we would expect 82 of each sex. In this case it looks as though there may be some discrepancy between the expected values and those actually found. This discrepancy could be entirely consistent with sampling variation—perhaps females are no more likely to choose biology and we ended up with a higher proportion by chance. The \(\chi^{2}\) goodness of fit test allows us to test how likely it is that such a discrepancy has arisen through sampling variation.
27.3.2 \(\chi^{2}\) contingency table test
A contingency table test is applicable in situations where each object is classified according to more than one categorical variable. Contingency table tests are usually used to test whether there is an association between the variables.
Consider biology students again. We might be interested in whether eye colour was in any way related to sex. It would be simple to record eye colour (e.g. brown vs. blue) along with the sex of each student in a sample. Now we would end up with a table that had two classifications:
| Blue eyes | Brown eyes | |
|---|---|---|
| Male | 44 | 20 |
| Female | 58 | 42 |
Now it is possible to compare the proportions of brown and blue eyes among males and females… The total number of males and females are 64 and 100, respectively. The proportion of males with brown eyes is 20/64 = 0.31, and that for females 42/100 = 0.42. It appears that brown eyes are somewhat less prevalent among males. A contingency table test will tell us if the difference in eye colour frequencies is likely to have arisen through sampling variation.
Notice that we are not interested in judging whether the proportion of males, or the proportion of blue-eyed students, are different from some expectation. That’s the job of a goodness of fit test. We want to know if there is an association between eye colour and sex. That’s the job of a contingency table test.
27.3.3 The assumptions and requirements of \(\chi^{2}\) tests
It’s important to realise that in terms of their assumptions, contingency tables and goodness-of-fit tests aren’t fundamentally different from one another. The difference between the two types lies in the type of hypothesis evaluated. When we carry out a goodness-of-fit test we have to supply the expected values, whereas the calculation of expected values is embedded in the formula used to carry out a contingency table test. That will make more sense once we’ve seen the two tests in action.
\(\chi^{2}\) tests are often characterised as non-parametric tests because they do not assume any particular form for the distribution of the data. In fact, as with any statistical test, there are some assumptions in play, but these are relatively mild:
The data are independent counts of objects or events which can be classified into mutually exclusive categories.
The expected counts are not very low. The general rule of thumb is that the expected values should be greater than 5.
The most important thing to remember about \(\chi^{2}\) tests is that they must always be carried out on the actual counts. Although the \(\chi^{2}\) is really telling us how the proportions of objects in categories vary, the analysis should never be carried out on the percentages or proportions, only on the original count data, nor can a \(\chi^{2}\) test be used with means.