Chapter 4 Data and variables
The truth is the science of nature has been already too long made only a work of the Brain and the Fancy. It is now high time that it should return to the plainness and soundness of Observations on material and obvious things.
Robert Hooke (1665)
The plural of anecdote is not data.
Roger Brinner
4.1 “Observations on material and obvious things”
As Hooke’s observation suggests, science cannot proceed on theory alone. The information we gather about a system stimulates questions and ideas about it and, in turn, can also allow us to test these ideas. In fact the idea of measuring and counting things is so familiar that it is easy to start a project without giving much thought to something as apparently mundane as the nature, quantity and resolution of the data we intend to collect. Nonetheless, the features of the data we collect determine both the types of analyses that can be carried out, and the confidence we can have in the conclusions drawn. We will spend a lot of time considering the statistical tools that can help us extract information from data, but no level of statistical sophistication will enable us to extract information that isn’t there to begin with.
So what is there to say about data? The first point to note is that, properly, the word data is the plural of datum (a single piece of information), so we should say “the data are…” not “the data is…”. That said, the use of the word in the singular is becoming more widespread, despite the objections of Grammar Nazis. The second, and much more important, point is that there are many different sorts of data. Examples include spatial maps of species’ occurrence and/or environmental factors, the DNA sequences of individuals, and networks of feeding relationships among species (i.e. food webs).
The data we collect in a study can be organised one or more statistical variables. In its loosest sense, statisticians use the word ‘variable’ to mean any characteristic that can be measured or experimentally controlled on different items or objects. People tend to think of variables as numeric quantities, such as height, but there is nothing to stop us working with non-numeric variables, such as colour. Collectively, a set of related variables are referred to as a data set (or just ‘the data’). Confused? Consider a concrete example: the spatial map example above. A minimal data set might comprise two variables containing the x and y position of sample locations, a third variable denoting the presence / absence of a species, and one or more additional variables containing information about the environmental factors we measured.
Data and variables in R
When using R, we often store a data set in a data frame. Each column in the data frame is one of R’s vectors — numeric, character, etc. The data are said to be tidy if the columns of the data frame correspond to the statistical variables in our data, and each row corresponds to a single observation. This simple connection between abstract statistical concepts and the concrete objects in R is not coincidence. R was designed first and foremost to analyse data.
4.2 Reading data into R
Last year we made extensive use of data sets that reside inside various R packages. This meant we could use the data without getting bogged down trying to read it into R. We don’t have the luxury of this short cut when we work with our own data, so we’ll adopt more realistic practices in this book. Whenever we need to work with a data set, we will have to first save a copy of it onto our computer, and then read it into R. All the data sets we use are stored as a Comma Separated Value (‘CSV’) text file. The read.csv function can be used to read in such files. The resulting data object in R is a data frame. A data frame is a table-like object that collects together different variables, storing each of them as a named column. We can access the data inside the data frame by referring to particular columns and rows, or manipulate the whole data frame with a package like dplyr.
If that last paragraph was confusing, it would be a good idea to work through the data frames chapter in the APS 135 course book.
4.3 Types of variable
When it comes to designing an experimental study or carrying out data analysis, it is very important to understand what sort of data we need, or have, as this affects what we can do with it. The variables in a data set can often be classified as being either numeric or categorical: numeric variables have values that describe a measurable quantity as a number, like ‘how many’ or ‘how much’; categorical variables have values that describe a characteristic of an observation, like ‘what type’ or ‘which category’. Numeric variables can be further characterised according to the type of scale they are measured on (interval vs. ratio scales). Categorical variables can be further characterised according to whether or not they have a natural order (nominal vs. ordinal variables).
4.3.1 Nominal (categorical) variables
Nominal variables arise when observations are recorded as categories that have no natural ordering relative to one other. For example:
| Marital status | Sex | Colour morph |
| Single | Male | Red |
| Married | Female | Yellow |
| Widowed | Black | |
| Divorced |
Variables of this type are common in surveys where, for example, a record is made of the ‘type of thing’ (e.g. the species) observed.
4.3.2 Ordinal (categorical) data
Ordinal variables occur where observations can be assigned some meaningful order, but where the exact ‘distance’ between items is not fixed, or even known. For example, if we are studying the behaviour of an animal when it meets another individual, it may not be possible to obtain quantitative data about the interaction, but we might be able to score the behaviours in order of aggressiveness:
| Behaviour | Score |
| initiates attack | 3 |
| aggressive display | 2 |
| ignores | 1 |
| retreats | 0 |
Rank orderings are a type of ordinal data. For example, the order in which runners finish a race (1st, 2nd, 3rd, etc.) is a rank ordering. It doesn’t tell us whether it was a close finish or not, but still conveys important information about the result.
In both situations we can say something about the relationships between categories: in the first example, the larger the score the more aggressive the response; in the second example the greater the rank the slower the runner. However, we can’t say that the gap between the first runner and the second was the same as between the second and third and we can’t say that a score of 2 is twice as aggressive as a score of 1 (though people sometimes make this kind of mistake).
How should you encode different categories in R?
We have to define some kind of coding scheme to represent the different categories of a nominal/ordinal variables in computerised form. It was once common to assign numbers to different categories (e.g. Female=1, Male=2). This method was sensible in the early days of computer-based data analysis because it allowed data to be stored efficiently. This efficiency argument is not really relevant on a modern computer. What’s more, there are good reasons to avoid coding categorical variables as numbers:
-
Numeric coding makes it harder to understand the raw data and to interpret the output of a statistical analysis of those data. This is because we have to remember which number is associated with each category. This is particularly problematic when a variable has many categories.
-
Numeric codes are arbitrary and should not be used as numbers in mathematical operations. In the above example, it is meaningless to say 2 [“male”] is twice the size of 1 [“female”].
R usually assumes that a variable containing numeric values is meant to be treated as a number. If we use numeric coding for a categorical variable, R will try to treat the offending variable as a number, which can lead to confusing errors. The take home message: Always use words (e.g., ‘female’ vs. ‘male’), not numbers, to describe categories in R.
4.3.3 Interval scale (numeric) variables
Interval scale variables take values on a consistent numeric scale, but where that scale starts at an arbitrary point. Temperature on the Celsius scale is a good example of interval data. We can say that 60\(^{\circ}\)C is hotter than 50\(^{\circ}\)C, and we can say that the difference in temperature between 60\(^{\circ}\)C and 70\(^{\circ}\)C is the same as that between -20\(^{\circ}\)C and -10\(^{\circ}\)C. We cannot say that 60\(^{\circ}\)C is twice as hot as 30\(^{\circ}\)C. This is because temperature on the Celsius scale has an artificial zero value—the freezing point of water. The idea becomes obvious when we consider that temperature can equally well be measured on the Fahrenheit scale (where the freezing point of water is 32\(^{\circ}\)F).
4.3.4 Ratio scale (numeric) variables
Ratio scale variables have a true zero and a known and consistent mathematical relationship between any points on the measurement scale. For example, there is a temperature scale that has a true zero: the Kelvin scale. Zero K is absolute zero, where matter actually has no thermal energy whatsoever. Temperature measurements in degrees K are on a ratio scale, i.e. it does make sense to say that 60 K is twice as hot as 30 K. Interval scale numeric variables are quite familiar, because the physical quantities that crop up in science are usually measured on a ratio scale: length, weight, and numbers of organisms are good examples.
Continuous or discontinuous? A common confusion with numeric data concerns whether the data are on continuous or discontinuous scales. Ratio data can be either. Many biological ratio data are discrete (i.e. only certain discrete values are possible in the original data), and therefore discontinuous. Count data are an obvious example, e.g. the number of eggs found in a nest, the number of plants recorded in a quadrat, or number of heartbeats counted in a minute. These can only comprise whole numbers, ‘in between’ values are not possible. However, the distinction between continuous and discontinuous data is often not clear cut – even ‘continuous’ variables such as weight are made discontinuous in reality by the fact that our measuring apparatus is of limited resolution (i.e. a balance may weigh to the nearest 0.01 g).
So… just keep in mind that the fact that data look (or really are) discontinuous does not mean they are necessarily ordinal data.
4.3.5 Why does the distinction matter?
The measurement scale affects what we can do (mathematically) to a numeric variable. We can add and subtract interval scale variables, but we can not divide or multiply them and arrive a meaningful result. In contrast, we can add, subtract, multiply or divide ratio scale variables. Put another way, differences and distances are meaningful for both interval and ratio scales, but ratios are only meaningful for ratio variables (the clue is in the name).
4.3.6 Which is best?
All types of data can be useful, but it is important to be aware that not all types of data can be used with all statistical models. This is one very good reason for why it is worth having a clear idea of the statistical tools we intend to use when designing a study.
In general, ratio variables are best suited to statistical analysis. However, biological systems often cannot be readily represented as ratio data, or the work involved in collecting good ratio data may be vastly greater than the resources allow, or the question we are interested in may not demand ratio data to achieve a perfectly satisfactory answer. It is this last question that should come first when thinking about a study. What sort of data do we need to answer the question we are interested in? If it is clear at the outset that data on a rank scale will not be sufficiently detailed to enable us to answer the question, then we must either develop a better way of collecting the data, or abandon that approach altogether. If we know the data we’re able to collect cannot address the question, then we should do something else.
An obvious, but important point: we can always convert measurements taken on a ratio scale to an interval scale, but we cannot do the reverse. Similarly, we can convert interval scale data to ordinal data, but we cannot do the reverse. That said, it’s good practise to avoid such conversions as they inevitably result in a loss of information.
4.4 Accuracy and precision
4.4.1 What do they mean?
The two terms accuracy and precision are used more or less synonymously in everyday speech, but in scientific investigation they have quite distinct meanings.
Accuracy – how close a measurement is to the true value of whatever it is you are trying to measure.
Precision – how repeatable a measure is, irrespective of whether it is close to the actual value.
If we are measuring an insect’s weight on an old and poorly maintained balance, which measures to the nearest 0.1 g, we might weigh the same insect several times and each time get a different weight — the balance is not very precise, though some of the measurements might happen be quite close to the real weight. By contrast you could be using a new electronic balance, weighing to the nearest 0.01g, but which has been incorrectly zeroed so that it is 0.2 g out from the true weight. Repeated weighing here might yield results that are identical, but all incorrect (i.e. not the true value) — the balance is precise, but the results are inaccurate. The analogy often used is with shooting at a target:
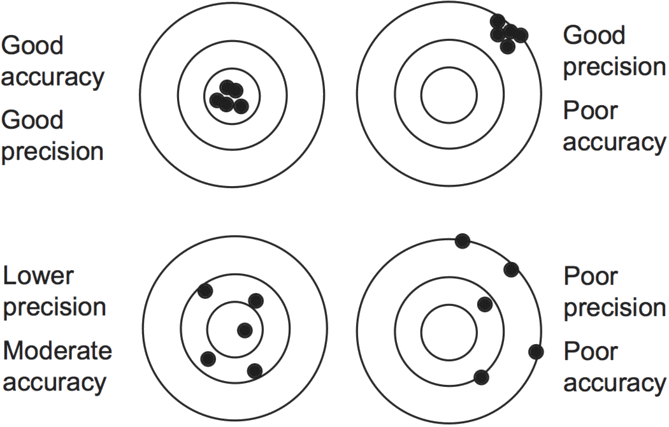
Figure 4.1: Accuracy and precision
It’s obviously important to know how accurate and how precise our data are. The ideal is the situation in the top left target in the diagram, but in many circumstances high precision is not possible and it is usually preferable to make measurements of whose accuracy we can be reasonably confident (bottom left), than more precise measurements, whose accuracy may be suspect (top right). Taking an average of the values for the bottom left target would produce a value pretty close to the centre; taking an average for the top right target wouldn’t help the accuracy at all.
4.4.2 Implied precision – significant figures
It’s worth being aware that when we state results, we’re making implicit statements about the precision of the measurement. The number of significant figures we use suggests something about the precision of the result. A result quoted as 12.375 mm implies the measurement is more precise than one quoted as 12.4 mm. A value of 12.4 actually measured with the same precision as 12.735 should properly be written 12.400. When quoting results, look at the original data to decide how many significant figures to use—generally the same number of significant figures will be appropriate.
These considerations do not apply in quite the same way when working with discrete data, e.g. precision of measurement is not an issue in recording the number of eggs in a nest. We use 4 not 4.0, but since 4 eggs implies 4.0 eggs it’s fine to quote average clutch size from several nests as 4.3 eggs. However, even with discrete data, if numbers are large then obviously precision is an issue again … a figure of 300 000 ants in a nest is likely to imply a precision of plus or minus 50 000. A figure of 320987 ants implies a rather improbably precise measurement.
4.4.3 How precise should measurements be?
The appropriate precision to use when making measurements is largely common sense. It will depend on practicality and the use to which we wish to put the data. It may not be possible to weigh an elephant to the nearest 0.001g, but if we want to know whether the elephant will cause a 10 tonne bridge to collapse, then the nearest tonne will be good enough. On the other hand, if we want to compare the mean sizes of male and female elephants then the nearest 100 kg may be sufficient, but if we plan to monitor the progress of a pregnant female elephant then the nearest 10 kg or less might be desirable.
As a rough guide aim, where possible, for a scale where the number of measurement steps is between 30 and 300 over the expected range of the data. So for example, in a study of the variation in shell thickness of dogwhelks on a 300 m transect up a shore, it would be adequate to measure the position of each sampling point on the transect to the nearest metre, but shell thickness will almost certainly need to be measured to the nearest 0.1 mm.
4.4.4 Error, bias and prejudice
Error is present in almost all biological data, but not all error is equally problematic. Usually the worst form of error is bias. Bias is a systematic lack of accuracy, i.e. the data are not just inaccurate, but all tend to deviate from the true measurements in the same direction (situations B and D in the ‘target’ analogy above). Thus there is an important distinction in statistics between the situation where the measurements differ from the true value at random and those where they differ systematically. Measurements lacking some precision, such as the situation illustrated in C, may still yield a reasonable estimate of the true value if the mean of a number of values is taken.
Avoiding bias in the collection of data is one of the most important skills in designing scientific investigations. Some forms of bias are obvious, others more subtle and hard to spot:
Non-random sampling. Many sampling techniques are selective, and may result in biased information. For example, pitfall trapping of arthropods will favour collection of the very active species that encounter traps most frequently. Studying escape responses of an organism in the lab may be biased if the process of catching organisms to use in the study selected for those whose escape response is poorest.
Conditioning of biological material. Organisms kept under particular conditions for long periods of time may become acclimatised to those conditions. Similarly, if stocks are kept in a laboratory for many generations their characteristics may change through natural selection. Such organisms may give a biased impression of the behaviour of the organism in natural conditions.
Interference by the process of investigation. Often the process of making a measurement itself distorts the characteristic being measured. For example, it may be hard to measure the level of adrenalin in the blood of a small mammal without affecting the adrenalin level in the process. Pitfall traps are often filled with a preservative, such as ethanol, but the ethanol attracts species of insect that normally feed on decaying fruit and use the fermentation products as a cue to find resources.
Investigator bias. Measurements can be strongly influenced by conscious or unconscious prejudice on the part of the investigator. We rarely undertake studies without some initial idea of what we are expecting, or we form ideas about the patterns we think we are seeing as the study progresses. For example, rounding up ‘in between’ values in the samples you are expecting to have large values and rounding down where a smaller value is expected, or having another ‘random’ throw of a quadrat when it doesn’t land in a ‘typical’ bit of habitat.
The ways in which biases, conscious and unconscious, can affect our investigations are many, often subtle, and sometimes serious. Sutherland (1994) gives an illuminating and sometimes frightening catalogue of the ways in which biases affect our perception of the world and the judgements we make about it. The message is that the results we get from an investigation must always be judged and interpreted with respect to the nature of the data used to derive them—if the data are suspect, the results will be suspect too.